
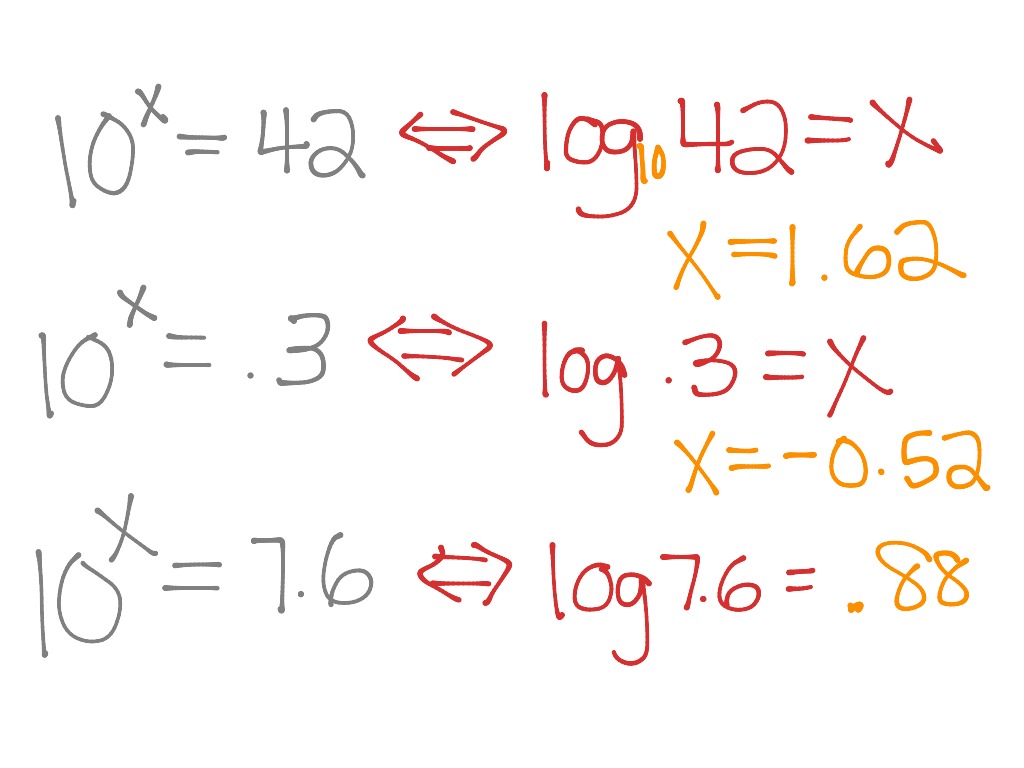
So now we've got 7 to 0 is equal to one, because any number of ways to the zero power is one Hi to the zero powers. Well, the only for us to get an excellent value to Equal Bun is if we raise that explode into a zero power. So then again, if we rewrite that using this rule right here. So we got in terms of reading that it would be right as log base seven of one is equal to X.

So for number two, we've got log base seven of one. So whenever you have, ah, positive base, you know that there's no way for you to get a negative number. That's how we know that this is going to be undefined. And so, in that sense as well, it's pretty clear that we could never have a negative value for our ext. Solving by substitution, u 2 - 1/v, thus. You know, it looks something like this, and there's an Essene took at, um X is equal to zero. Finding an antilog is the inverse operation of finding a log, so is another name for exponentiation. It does not work and even is by considering the graph of Log of X. So that means that it could never become negative, meaning that this value right here is undefined. Every other graph y is equal to three to the X power. Well, we know that in terms of the graph oven exponents, it looks something like this, and there's an ascent took at zero. When will we ever have, um, a negative number when we're raising an ex wanted to value a positive export into a value. Then that means that we could say that three to the X power is equal to negative two. So what I like to do is I like to rewrite it in terms of an exponent, because we know that if we have this log based a F B is equal to see, you know, we could rewrite the southern exponents to say eight. I personally think that dealing with logs is pretty tricky for most people because it is an operation that were not very used to. And so one easy way to think about what this would become. It is how many times we need to use 10 in a multiplication, to get our desired number.
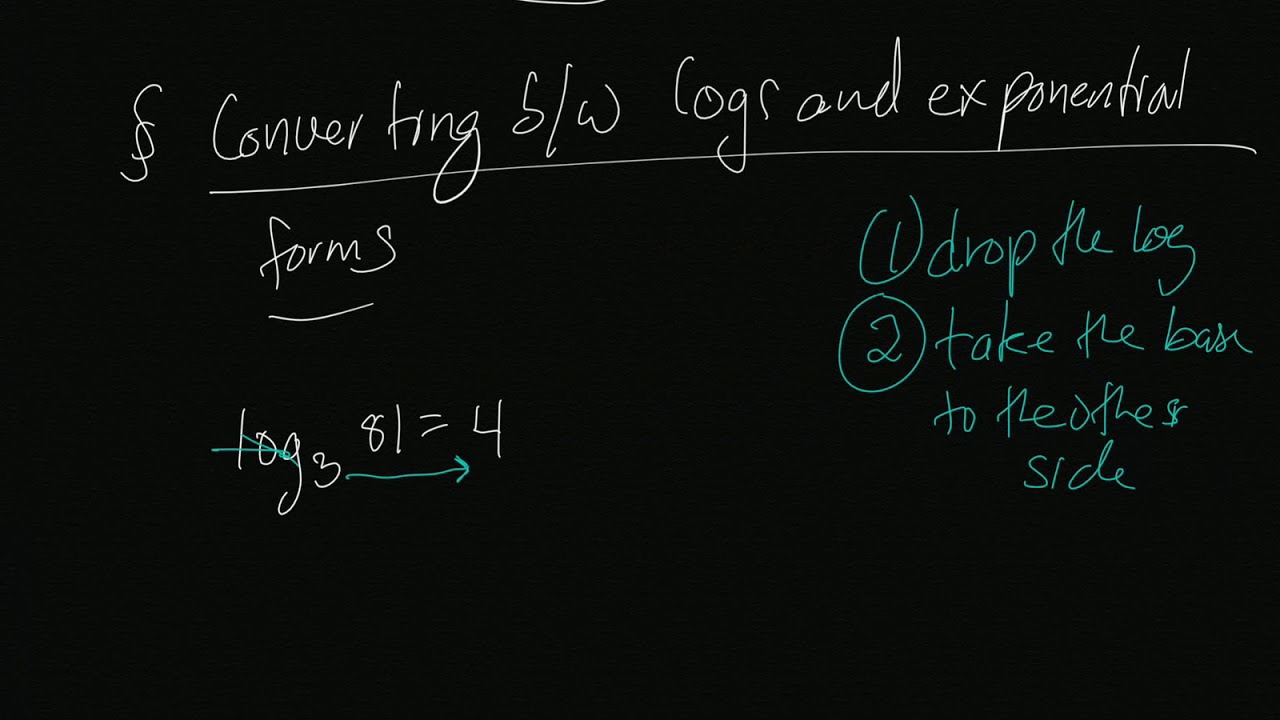
Okay, then we have locked these three of negative, too. Sometimes a logarithm is written without a base, like this: log (100) This usually means that the base is really 10. So for the first one, we've got logged based three of native to So just keep in mind that in terms of reading it, we would read it as log base. Siri's X one, and it just has to evaluate. Okay, so this is gonna be the first example out of our evaluating lock rhythms. When evaluating a log without a calculator, you can use the addition property of logs, the subtraction property of logs, the exponential property, the power property, and/or the logarithm of a.


 0 kommentar(er)
0 kommentar(er)
